Lattice Model of Information Flow

I am caught in a maelstrom of work and so I decide to play.

I have an excellent textbook on discrete mathematics on my shelf from a course I took as a student a few years ago [1]. Its always useful to review such books to remind oneself of certain foundational principles used in computer science [2]. My thesis work concerns, among other things, the study of information flow and in the course of my work I found myself consulting this book to review the mathematical concept of a lattice [3]. Looking through the index of this text I found an entry reading 'Information flow, lattice model of, 525'. Naturally, I was intrigued.

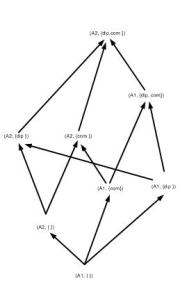
Funnily enough, the three paragraph section on the lattice model of information flow is only of tangential relevance to my thesis work; yet it was interesting enough. It discussed the uses of lattices to model security policies of information dissemination. Rosen presented a simple model of a multi-level security policy in which a collection data (the authors use the word information) is assigned an authority level A, and a category C. The security class of a collection of data is modeled as the pair \( (A,C)\). Rosen defines a partial order on security classes as follows: \( (A_{1},C_{1})\preceq (A_{2},C_{2})\) if and only if \( A_{1} \leq A_{2}\) and \( S_{1} \subseteq S_{2}\). This is easily illustrated by an example.

Let \( A = \{A_{1}, A_{2}\}\) where \( A_{1} \leq A_{2}\) and \( A_{1}\) is the authority level secret and \( A_{2}\) is the authority level top secret. Let \( S=\{diplomacy, combat ops \}\) [4][5]. This forms the lattice depicted in figure 1.

The objective of such a security policy is to govern flows of sensitive information. Thus, if we assign individuals security clearances in the same way that information is assigned security classes, then we can set up a policy such that an item of information i assigned a security class \( (A_{1},C_{1})\) can only be disseminated to an individual a having security clearance \( (A_{2},C_{2})\) if and only if \( (A_{1},C_{1})\preceq (A_{2},C_{2})\).

Without looking at the literature [6], it seems that the obvious next step is to embed this into a network model. Supposing that one has a network model in which each node is classified by a security clearance there are a variety of useful and potentially interesting questions that can be asked. For example, one might want to look for connected components where every node in the connected component has a security clearance \( (A,C)\) such that \( (A,C)\succeq (A_{j},C_{k})\) for some j and k. Or if one were interested in simulating the propagation of information in that social network such that the probability of a node communicating certain security classes of information to another node is a function of the security class of the information and the security clearances of those two nodes.

So far this discussion has limited itself to information flow as dissemination of information vehicles, contrary to the direction I suggested in my last post should be pursued. One easy remedy might be to have minimally cognitive nodes with knowledge bases and primitive inference rules by which new knowledge can be inferred from existing or newly received items of information. This would have several consequences. Relevant items of novel information might disseminate through the network (and global knowledge grows), and items of information not originally disseminated, for example because it is top secret, may yet be guessed or inferred from existing information by nodes with security clearances too low to have received it normally.

Moving away from issues of security policy, we can generalize this to classify nodes in social networks in other systematic ways. In particular, we may be interested in epistemic communities. We might classify beliefs and/or knowledge using formal tools like formal concept analysis, as I believe Camille Roth has been doing (e.g. see his paper Towards concise representation for taxonomies of epistemic communities).

Fun stuff.

[1] Rosen, Kenneth H. Discrete mathematics and its applications. 5th edition. McGraw Hill. 2003.

[2] Some undergraduates joked that if they mastered everything in Rosen's book, they would pretty much have mastered the foundations of computer science. An exaggeration, but not far off.

[3] A lattice is a partially ordered set (poset) such that for any pair of elements of that set there exists a least upper bound and a greatest lower bound.

[4] According to Wikipedia such the US uses classifications like the following:

1.4(a) military plans, weapons systems, or operations;

1.4(b) foreign government information;

1.4(c ) intelligence activities, sources, or methods, or cryptology;

1.4(d) foreign relations or foreign activities of the United States, including confidential sources;

1.4(e) scientific, technological or economic matters relating to national security; which includes defense against transnational terrorism;

1.4(f)USG programs for safeguarding nuclear materials or facilities;

1.4(g) vulnerabilities or capabilities of systems, installations, infrastructures, projects or plans, or protection services relating to the national security, which includes defense against transnational terrorism; and

1.4(h) weapons of mass destruction.

[5] An interesting category of information is information about who has what security clearance.

[6] Where fun and often good ideas go to die.